Protocols for overlaps

The Overlap of the two quantum states \(\ket{\Psi_0}\) and \(\ket{\Psi_1}\) with a kernel \(\hat{A}\) is, in general, a complex number given by

(44)\[\langle \Psi_0 | \hat{A} | \Psi_1 \rangle\]

where \(\hat{A}\) is a QubitOperator i.e. it is written as a linear combination of Pauli strings \(\hat{A} = \sum_i c_i P_i\), and may be an identity. InQuanto supports shot-based calculations of overlaps with the HadamardTestOverlap, SwapFactorizedOverlap, and ComputeUncomputeFactorizedOverlap protocols, discussed below.

HadamardTestOverlap

Let \(\ket{\Psi_0} = U_0 \ket{\bar{0}}\) and \(\ket{\Psi_1} = U_1 \ket{\bar{0}}\), where \(U_0\) and \(U_1\) are state preparation unitaries. The HadamardTestOverlap protocol uses a “linear combination of unitaries” approach with a single ancilla on which to control the state preparation unitaries [30]. This protocol offers two measurement options: direct=False, where measurement is performed on the ancilla qubit only, and direct=True, where measurement is performed on both the ancilla and state registers [31]. First, we discuss the direct=False case.

To calculate the real part of the overlap, \(\text{Re}\langle \Psi_0 | \Psi_1 \rangle\), a single circuit is required which takes the form:

Fig. 12 Measurement circuit for the real part of the overlap with identity kernel, generated by the HadamardTestOverlap protocol with direct=False. The first qubit is the ancilla and the remaining qubits comprise the state register.

This circuit prepares the quantum state:

(45)\[\frac{1}{2}\left[ |0\rangle \otimes |\Psi_0 + \Psi_1\rangle + |1\rangle \otimes |\Psi_0 - \Psi_1\rangle \right]\]

where the first ket in each term is the ancilla, and \(|\Psi_0 \pm \Psi_1\rangle = (U_0 \pm U_1)|\bar{0}\rangle\) is the state register. Given this state, the real part of the overlap is given by \(\text{Re}\langle \Psi_0 | \Psi_1 \rangle = p(0) - p(1)\), where \(p(b)\) is the probability of measuring the ancilla qubit in the state \(b\). To compute the imaginary part of the overlap, a similar circuit is required with a small modification compared to the circuit above:

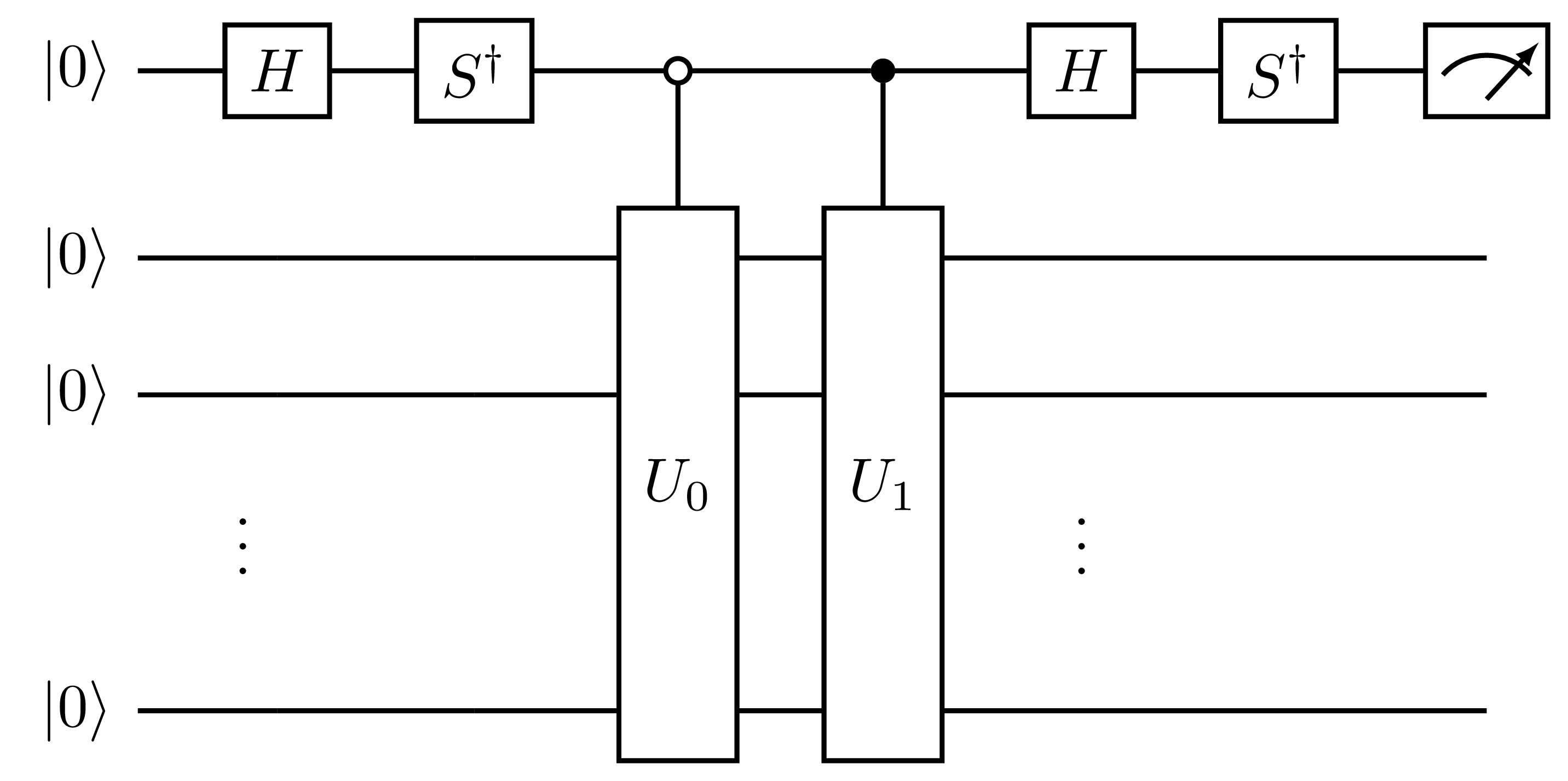
Fig. 13 Measurement circuit for the imaginary part of the overlap with identity kernel, generated by the HadamardTestOverlap protocol with direct=False.

and the imaginary part is given equivalently by \(\text{Im}\langle \Psi_0 | \Psi_1 \rangle = p(0) - p(1)\).

For an overlap with a kernel \(\hat{A}=\sum_i c_i P_i\), we may write:

(46)\[\langle \Psi_0 | \hat{A} | \Psi_1 \rangle = \sum_i c_i \langle \Psi_0 | P_i | \Psi_1 \rangle = \sum_i c_i \langle \Psi_0 | \Psi_1^i \rangle\]

where each Pauli word has been appended to the \(| \Psi_1 \rangle\) state preparation; \(| \Psi_1^i \rangle = P_i U_1 |\bar{0}\rangle\). Each term in this sum is then computed independently as described above. Thus, with direct=False, to compute the complex overlap with a kernel of \(N\) terms, \(2N\) circuits are required.

In the direct=True case, the Pauli words in \(\hat{A}\) are partitioned into simultaneously measurable sets (commuting sets, for example). Measurement circuits for each set are then appended to the end of the state register, similarly to the Pauli averaging protocol. These circuits take the form:

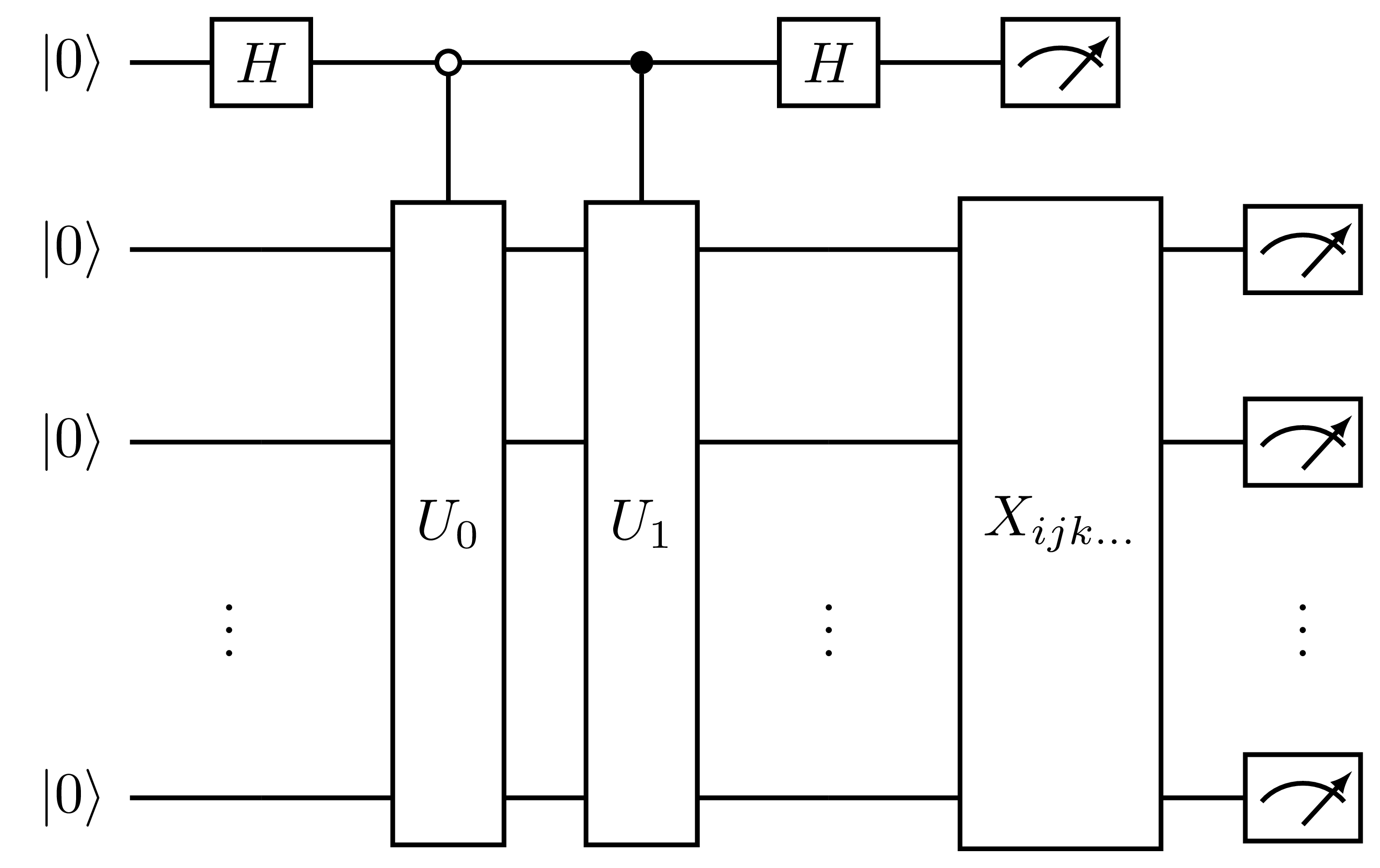
Fig. 14 Measurement circuit for the real part of the overlap, generated by HadamardTestOverlap with direct=True, where \(X_{ijk\dots}\) is the set of circuits required to measure the matrix elements of a set of simultaneously measurable Pauli words. The first qubit is the ancilla and the remaining qubits comprise the state register.

In this case, measurement of the state register measures \(\langle \Psi_0 + \Psi_1 | P_i | \Psi_0 + \Psi_1 \rangle\) when the ancilla is \(|0\rangle\), and \(\langle \Psi_0 - \Psi_1 | P_i | \Psi_0 - \Psi_1 \rangle\) when the ancilla is \(|1\rangle\). By taking a linear combination of these outcomes we can retrieve \(\langle \Psi_0 | P_i | \Psi_1\rangle\). Thus, with direct=True, to compute the complex overlap with a kernel we require \(2N_p\) circuits, where \(N_p\) is the number of simultaneously measurable sets of Pauli words in the kernel.

A simple example of using this protocol is given below:

 from inquanto.operators import QubitOperator
 from inquanto.states import QubitState, FermionState
 from inquanto.ansatzes import FermionSpaceAnsatzUCCSD, HardwareEfficientAnsatz
 from inquanto.computables import Overlap
 from inquanto.protocols import HadamardTestOverlap
 from pytket import OpType
 from pytket.extensions.qiskit import AerBackend
 from pytket.partition import PauliPartitionStrat

 bra = HardwareEfficientAnsatz([OpType.Rx, OpType.Ry], QubitState([1, 1, 0, 0]), 2)
 ket = FermionSpaceAnsatzUCCSD(4, FermionState([1, 1, 0, 0], 1))
 params = (
      bra.state_symbols.construct_random()
      | ket.state_symbols.construct_random()
 )
 kernel = QubitOperator.from_string("(-0.1, Z0), (0.1, Z1), (0.25, X0 X1)")

 ovlp = Overlap(bra, ket, kernel)

 protocol = HadamardTestOverlap(
   AerBackend(),
   shots_per_circuit=int(12e3),
   direct=True,
   pauli_partition_strategy=PauliPartitionStrat.CommutingSets
)
protocol.build_from(params, ovlp)
protocol.compile_circuits()
protocol.run(seed=0)

circs = protocol.get_circuits()
print("Num circuits: ", len(circs))
print("Circuit 0 depth: ", circs[0].depth())

ovlp.evaluate(protocol.get_evaluator())

Num circuits:  4
Circuit 0 depth:  217

np.complex128(-0.04965+0.024458333333333332j)