H2 Operation¶
QCCD Operation¶
System Model H2 is a transport-based quantum processor with a linear race-track geometry. Random qubit access utilizes all 8 gate zones as swapping regions. The periodic boundary conditions of the device are explicitly taken into account and the transport operations are computed using a parallel bubble sort routine that allows qubits to move in both directions around the device. layers of the circuit are executed sequentially, with transport primitives used to arrange the ions so that qubits scheduled to be gated in a given layer are positioned next to each other
State Preparation and Measurement (SPAM) is only possible in the 4 gate zones. During 32-qubit operation (2-qubit gates on all \(\left[(N/2)\right]\) pairs), the ions can be grouped into four “batches” of 8, with the four batches occupying the Down Gate (DG) zones, Upper Gate (UG) zones, and each of the two storage regions. During ion transport, we cool all \(^{138}\)Ba\(^+\) ions with Doppler cooling “sheet beams”.
Measurement operations are performed in the DG zones using state-dependent resonance fluorescence. Mid-circuit measurement and reset (MCMR) causes a small crosstalk error that acts on neighboring qubits due to stray light from the measurement and reset beams. For unmeasured ions in the gate zones, this error is mitigated by the micromotion hiding technique.
Qubit Species¶
System Model H2 encodes the computational space into the 2\(S_{\frac{1}{2}}\) spin manifold of a \(^{171}\)Yb\(^{+}\) ion. (\(^{138}\)Ba\(^{+}\)) is used as the sympathetic cooling ion. The \(|0 \rangle\) is defined as \(| 2S_{\frac{1}{2}}, F = 0, m_{F} = 0 \rangle\). The \(|1 \rangle\) is defined as \(| 2S_{\frac{1}{2}}, F = 1, m_{F} = 0 \rangle\).
Native Gate Set¶
Quantinuum Hardware utilizes the following native gate set. The TKET definitions are in units of \(\pi\), but the formulas in the middle column are defined in radians.
Gate |
Expression |
TKET |
Native 1-qubit gates |
||
\(R_{xy} (\theta, \phi)\) |
\(e^{ \frac{-i \theta}{2} \left(\cos(\phi) \hat{X} + \sin(\phi) \hat{Y}\right) }\) |
|
\(R_{z}(\lambda)\) |
\(e^{-i \frac{\lambda}{2} \hat{Z}}\) |
|
Fully entangling 2-qubit gates |
||
\(ZZ()\) |
\(e^{-i \frac{\pi}{4} \hat{Z} \bigotimes \hat{Z}}\) |
|
Parameterized angle 2-qubit gates |
||
\(R_zz(\theta)\) |
\(e^{-i \frac{\theta}{2} \hat{Z} \bigotimes \hat{Z} }\) |
|
General SU(4) entangler |
||
\(R_{xxyyzz} (\alpha, \beta, \gamma)\) |
\(e^{\frac{-i}{2} (\alpha \hat{X} \bigotimes \hat{X} + \beta \hat{Y} \bigotimes \hat{Y} + \gamma \hat{Z} \bigotimes \hat{Z})}\) |
|
\(\hat{X}\), \(\hat{Y}\) and \(\hat{Z}\) are the standard Pauli operators, and the two-qubit matrix is written in the \(|0,0 \rangle\), \(|0,1 \rangle\), \(|1,0 \rangle\), \(|1,1 \rangle\) basis.
The parameterized rotation around the \(z\)-axis, \(R_z\) (\(\lambda\)), is performed virtually within the software. All other physical gates are constructed from this set.
By default, quantum circuits submitted to the hardware are rebased to the fully entangling \(ZZ\) gate and the parameterized \(R_{zz}\) gate. Circuits are rebased to the \(R_{xxyyzz}(\alpha, \beta, \gamma)\) only if users specify this option at job submission. The minimum gate angles for the \(R_{zz}\) gate angle is \(1 \times 10^{-4}\) and the minimum \(R_{xy}\) gate angle is \(3 \times 10^{-4}\). Gates angles smaller are automatically rounded to zero.
Rebasing Quantum Circuits¶
Quantum circuits are rebased to the Quantinuum native gate set as described below.
Gate |
Rebase |
Pauli gate: bit-flip |
\(\sigma_x = R_{xy} (\pi,0)\) |
Pauli gate: bit and phase flip |
\(\sigma_y = R_{xy} (\pi,\pi/2)\) |
Pauli gate: phase flip |
\(\sigma_z = R_z(\pi)\) |
Clifford gate: Hadamard |
\(H = R_{xy} (\pi/2,-\pi/2)\) |
\(R_z(\pi)\) |
|
Clifford gate: CNOT |
\(CX^{(c,t)} = R_{xy}^{(t)}(-\pi/2,\pi/2)\) |
\(ZZ\) |
|
\(R_{z}^{(c)}(-\pi/2)\) |
|
\(R_{xy}^{(t)}(\pi/2,\pi)\) |
|
\(R_{z}^{(t)}(-\pi/2)\) |
|
Pauli interaction: Z basis |
\(R_{zz}(\pi/4) = R_{zz}(\pi/4)\) |
Pauli interaction: X basis |
\(R_{xx}(\pi/4) = R_{xy}^{(c)}(\pi/2,\pi/2)\) |
\(R_{xy}^{(t)}(\pi/2,\pi/2)\) |
|
\(R_{zz}(\pi/4)\) |
|
\(R_{xy}^{(c)}(\pi/2,-\pi/2)\) |
|
\(R_{xy}^{(t)}(\pi/2,-\pi/2)\) |
Hardware Compilation¶
A compiler generates a schedule of quantum gates and transport operations with the goal of minimizing the total transport time required to execute the circuit. The circuit is first decomposed into layers, which are built iteratively by looking ahead through the circuit and grouping together (into one layer) the largest possible set of 2-qubit gates subject to two constraints: (1) no ions participate in more than one gate in each layer, and (2) the time ordering of 2-qubit gates that share one or more qubit (or any time-ordering enforced by an explicitly requested barrier) is respected. The circuit is then converted into a layered directed acyclic graph
Mid-circuit Measurement and Conditional Operations¶
Due to the internal level structure of trapped-ion qubits, a mid-circuit measurement may leave the qubit in a non-computational state. All mid-circuit measurements should be followed by initialization if the qubit is to be used again in that circuit. The qubit may be prepared in the measured state by calling for a measurement followed by initialization and a measurement dependent spin-flip.
When a subset of qubits is measured in the middle of the circuit, the classical information from these measurements can be used to condition future elements of the circuit. Although the laser pulses that implement both 1- and 2-qubit gates are conditional, the transport operations used to rearrange the physical location of the qubits are not. The qubits will be reconfigured to allow for all gates in all branches irrespective of the mid-circuit measurement outcome. In the context of memory error and run time, the effective depth of a circuit with measurement conditioned branching includes all branches.
A discussion on mid-circuit measurement and reset consumption with pytket is available here.
Hardware Credit Limitations¶
Each shot submitted to hardware has a 50 HQC hard limit. Each job submitted to hardware is limited to 10,000 shots (500,000 HQC hard limit). These cost restrictions ensure the chunk duration for each job does not exceed the maximum allowable interval between system checks, calibrations, and validations while ensuring system performance. Users are encouraged to contact Quantinuum to increase their HQC limits per shot.
Parameterized Angle ZZ Gates¶
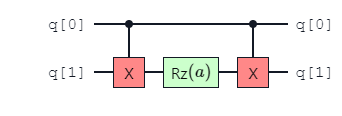
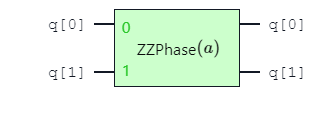
Although a parameterized angle 2-qubit entangling gate can be constructed using two fixed-angle 2-qubit entangling gates, a direct implementation will lower the error rate in the circuit. Not only is the number of entangling gates reduced, but the error of an \(R_{ZZ}(\theta)\) gate also scales with the angle \(\theta\) [1]. The error on \(R_{zz}(\frac{\pi}{2})\) is equal to the error of \(ZZ()\).
The gate sequence \(CX\), \(R_{z}\), \(CX\) can be replaced with the parameterized angle \(ZZ\) gate. This enables a lower number of 2-qubit gates in a quantum circuit, improving performance by decreasing gate errors.
For a narrative on parameterized angle gate usage, please see parameterized 2-qubit gates.
Real-time Classical Computation¶
The control system (ARM cortex processor) supports boolean and integer arithmetic. Floating point arithmetic is not supported. Additionally, the control system supports forward branching. This can be used to skip gating operations.
Real-time QEC Decoding¶
A co-located low-latency, high-performance classical compute environment enables execution of user-defined table-driven or algorithmic QEC (Quantum Error Correction) decoders during the coherence time of qubits [1]. The classical compute environments uses a Wasm runtime, including a Wasm Virtual Machine (WAVM). It offers near-native execution speeds of custom decoders without requiring full-system modification. This environment is sand-boxed to protect against untrusted user code submitted for execution. The classical compute environment offers users 16 GB RAM and leverages an Intel Kabylake processor, however parallelization is not possible with the Wasm runtime on H2. Wasm execution requires network call from the control system to the classical compute environment. A document on real-time QEC decoding is available here.