System Benchmarks¶
System-level benchmarks are general indicators of performance for hard problems. However, unlike component-level benchmarks, failure of specific operations are not reported directly.
Quantum Volume¶
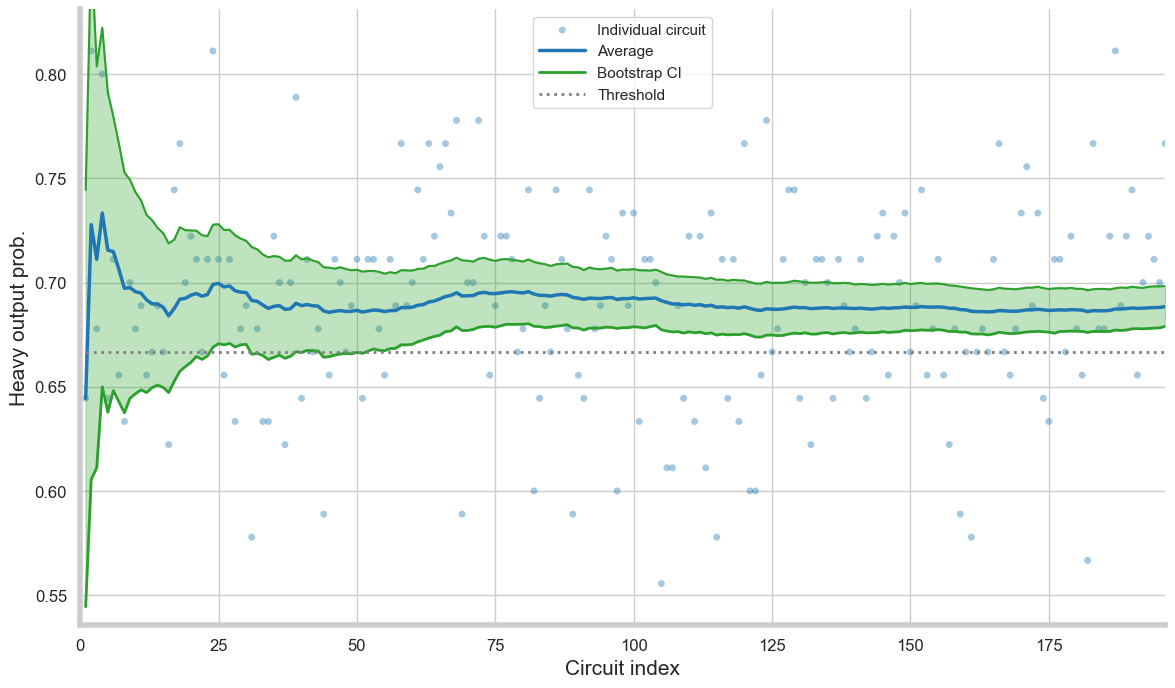
The quantum volume (QV) test is a full system-level benchmark for quantum computers that is sensitive to qubit number, fidelity, connectivity, and other quantities believed to be important in building useful devices [1]. QV require time consuming and extensive classical processing.
Quantum volume prescribes a set of test circuits that involve pairing of \(n_q\) qubits, applying a 2-qubit gate randomly selected from \(SU(4)\), and repeating this process for n_q rounds. Each circuit is run on the quantum computer and then compared to a full statevector classical simulation of the ideal circuit with a heavy output probability (HOP) test. The process is repeated with at least 100 circuits and if the average HOP over the set of circuits is above 2/3 with two-sigma confidence the test is passed and the system has quantum volume = \(2^{n_q}\).
Quantum Volume improvements on Quantinuum systems from 2020 to 2024.¶
GHZ State Fidelity¶
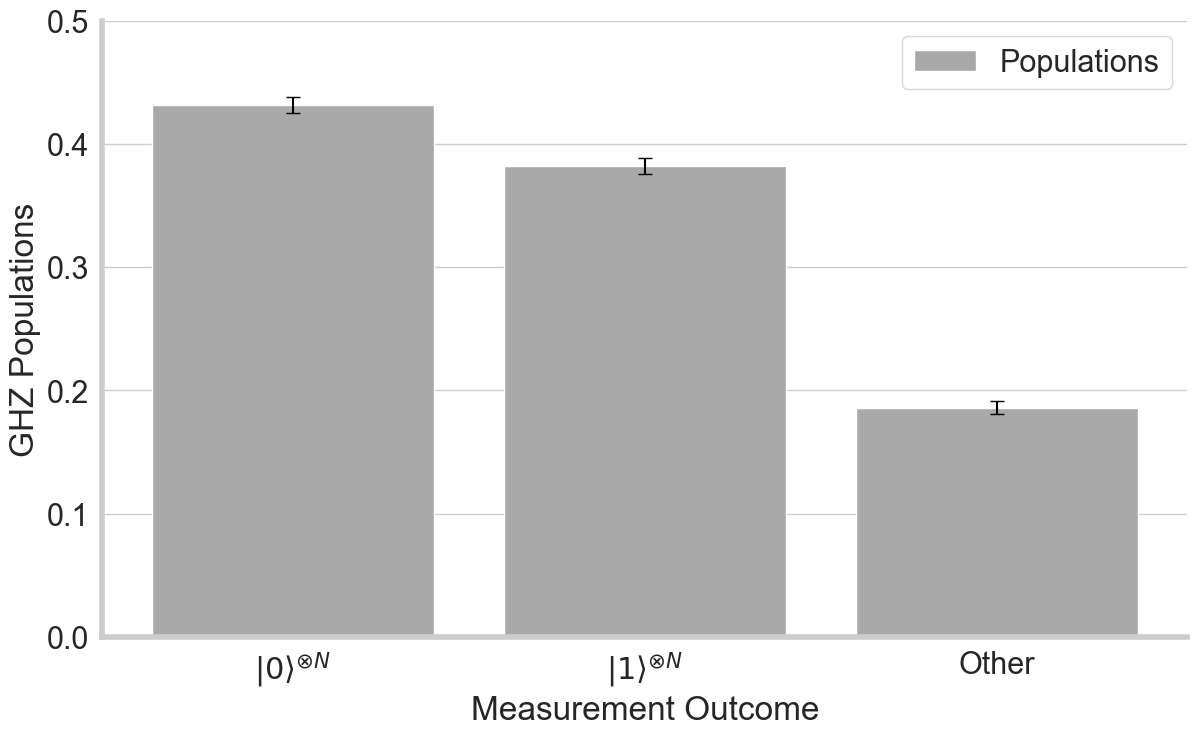
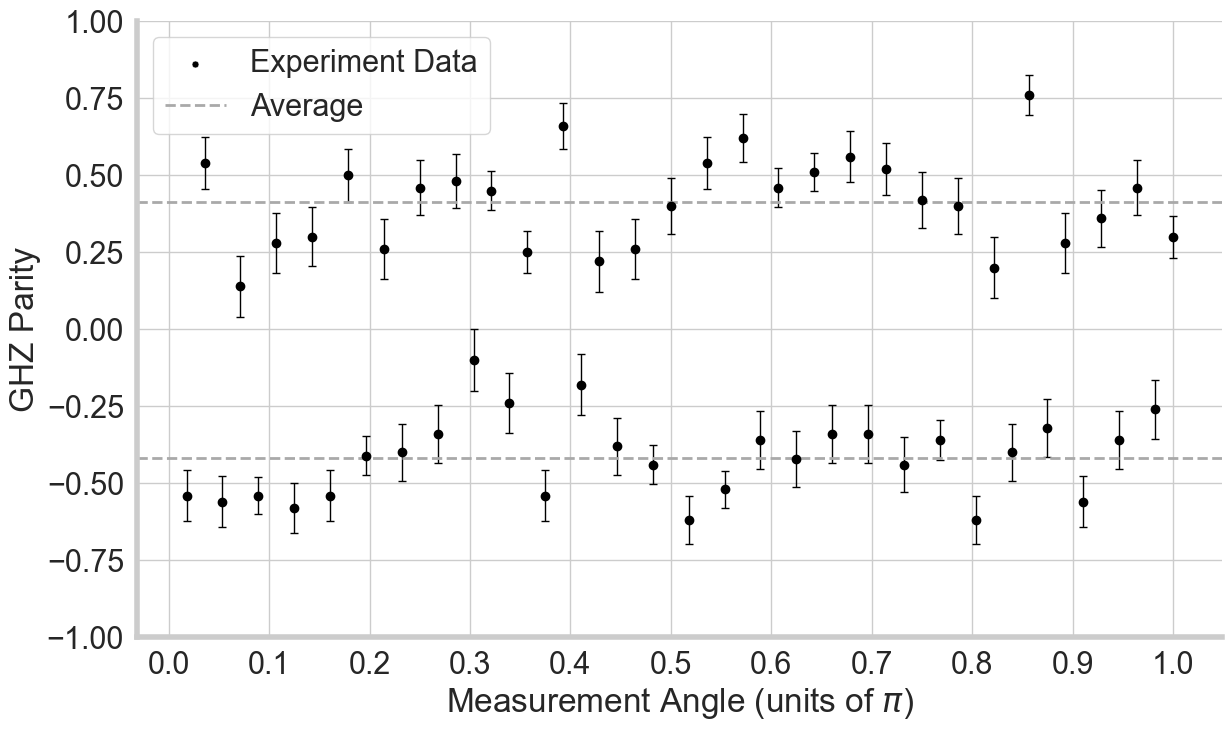
Greenberger–Horne–Zeilinger (GHZ) State Fidelity Estimation measures the ability of a system to create large, entangled states. We use the logarithmic-depth GHZ state perpation protocol and estimate the state fidelity by measuring populations and coherences of the state [2][3]. A measured state fidelity greater than 0.5 indicates the state has genuine n-body entanglement. In our benchmark we do not use any SPAM correction.
The data from H2-1 is plotted below for 56 qubits giving a fidelity of \(0.6156\pm0.0082\). The population measurement is ideally 50:50 split between \(|0 \rangle^{\bigotimes N}\) and \(|1 \rangle^{\bigotimes N}\) states. On the H2-1 device, the probability of measuring a different state is 0.2. The probability of measuring the all-ones state is worse than all-zeros state due to assymetry in spam error. The parity measurement quantifies the degree of superposition and ideally oscillates from 1 to -1 with period equal to \(\frac{\pi}{N}\) for \(N\) qubits. A parity of zero implies no superposition in the GHZ state.
A discussion of the GHZ state is available here.
