Helios Operation¶
QCCD Operation¶
The Helios QPU is a transport-based quantum processor with spatially separate qubit storage regions (memory and cache) and quantum logic regions. The storage zone is a ring that can be rotated to access qubit via junction transport . The junction is composed of two radiofrequency (RF) Paul traps and offers an order of magnitude speed-up accessing qubits relative to a single swapping zone via a bubble sort algorithm. Random access memory in Helios architecture provides huge gains in routing time to plan dynamically in response to Mid-circuit Measurements & Reset (MCMR). There is a speed and scaling advantage to junction transport. The junction enables all-to-all connectivity with \(N\) operations compared to \(N^2\) for swaps. Qubits can be sorted with a single signal per junction, not possible in swaps .
The quantum logic region processes batches of up to 16 qubits at a time, using 8 high-fidelity operation zones, each with the capability to perform state preparation, measurement, ground-state laser cooling, and quantum logic gates. This system requires 7 gating rounds to perform 2-qubit gates on all \(\left[(N/2)\right]\) pairs for a maximally dense circuit.
Visual schematic of the Helios trap.
Qubit Species¶
Quantinuum Helios encodes the computational space into the 2\(S_{\frac{1}{2}}\) spin manifold of a non-radioactive Barium ion (\(^{137}\)Ba\(^{+}\)). \(^{171}\)Yb\(^{+}\) is used as the sympathetic cooling ion. The \(|0 \rangle\) is defined as \(| 2S_{\frac{1}{2}}, F = 1, m_{F} = 0 \rangle\). The \(|1 \rangle\) is defined as \(| 2S_{\frac{1}{2}}, F = 2, m_{F} = 0 \rangle\). Barium puts all the critical transitions in the visible wavelength range (or longer), which is much more amenable to integrating into Helios and beyond. Visible light is also easier to manage the larger laser powers that result in higher fidelity 2-qubit gates. Moving to visible transitions allows for use of industrial laser products with component choices that are more mature, reliable, and cost-effective than the ultra-violet transitions required in our previous qubit species. Using more available laser power with better phase performance, we can suppress the leading source of errors in quantum logic gate implementations.
Native Gate Set¶
Quantinuum hardware utilizes the following native gate set. All gate angles are defined in radians.
Gate |
Expression |
Guppy |
\(R_{xy} (\theta, \phi)\) |
\(e^{ \frac{-i \theta}{2} \left( \cos(\phi) \hat{X} + \sin(\phi) \hat{Y}\right)}\) |
|
\(R_{z}(\lambda)\) |
\(e^{-i \frac{\lambda}{2} \hat{Z}}\) |
|
\(ZZ()\) |
\(e^{-i \frac{\pi}{4} \hat{Z} \bigotimes \hat{Z}}\) |
|
\(R_{ZZ}(\theta)\) |
\(e^{-i \frac{\theta}{2} \hat{Z} \bigotimes \hat{Z} }\) |
|
\(M(\rho)\) |
\(| 0 \rangle \langle 0 | \rho | 0 \rangle \langle 0 | + | 1 \rangle \langle 1 | \rho | 1 \rangle \langle 1 |\) |
|
\(R(\rho)\) |
\(| 0 \rangle \langle 0 | \rho | 0 \rangle \langle 0 | + | 0 \rangle \langle 1 | \rho | 1 \rangle \langle 0 |\) |
|
The parameterized rotation around the \(z\)-axis, \(R_z\) (\(\lambda\)), is performed virtually within the software. All other physical gates are constructed from this set. By default, quantum circuits submitted to the hardware are rebased to the fully entangling \(ZZ\) gate and the parameterized \(R_{ZZ}\) gate. The minimum gate angles for the \(R_{zz}\) gate angle is \(1 \times 10^{-4}\) and the minimum \(R_{xy}\) gate angle is \(3 \times 10^{-4}\). Gates angles smaller are automatically rounded to zero.
Decompostions¶
The tket compiler is responsible for realignment of non-native operations into native operations after job submission to hardware. The function guppy:guppylang.std.angles.angle() is used to define gate angles.
angle(1)= \(\pi\)angle(0.5)= \(\frac{\pi}{2}\)
Gate |
Decomposition |
|---|---|
|
See below |
|
See below |
|
See below |
|
See below |
|
See below |
|
See below |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The decompositions are reported in terms of guppy gate operations from the qsystem submodule, . Gate parameters are reported as instances of angle.
Toffoli gate (CCX)¶
toffoli(control1: qubit, control2: qubit, target: qubit) is decomposed to
phased_x(target: qubit, angle(1), angle(-0.5))
zz_phase(control2: qubit, target: qubit, angle(0.5))
phased_x(target: qubit, angle(0.25), angle(0.5))
zz_phase(control1: qubit, target: qubit, angle(0.5))
phased_x(target: qubit, angle(0.25), angle(0))
zz_phase(control2: qubit, target: qubit, angle(0.5))
phased_x(target: qubit, angle(0.25), angle(-0.5))
zz_phase(control1: qubit, target: qubit, angle(0.5))
phased_x(control1: qubit, angle(1), angle(0.25))
phased_x(target: qubit, angle(-0.75), angle(1))
zz_phase(control1, control2, angle(0.25))
rz(target, angle(1))
phased_x(control1: qubit, angle(1), angle(-0.25))
rz(control2: qubit, angle(-0.75))
rz(control1: qubit, angle(0.25))
Controlled H gate (CH)¶
ch(control: qubit, target: qubit)
phased_x(target: qubit, angle(-0.25), angle(0.5))
zz_phase(control: qubit, target: qubit, angle(0.5))
rz(control: qubit, angle(-0.5))
rz(target: qubit, angle(-0.5))
phased_x(target: qubit, angle(0.25), angle(0.5))
Controlled CRz gate (CRz)¶
crz(control: qubit, target: qubit, a: angle)
zz_phase(control: qubit, target: qubit, -a/2)
rz(target: qubit, a/2)
Controlled X gate (CX)¶
cx(control: qubit, target: qubit) is decomposed to
phased_x(target: qubit, angle(-0.5), angle(0.5))
zz_phase(control: qubit, target: qubit, angle(0.5))
rz(control: qubit, angle(-0.5))
phased_x(target: qubit, angle(0.5), angle(1))
rz(target: qubit, angle(-0.5))
Controlled Y gate (CY)¶
cx(control: qubit, target: qubit) is decomposed to
phased_x(control: qubit, angle(1), angle(1))
phased_x(target: qubit, angle(-0.5), angle(1))
zz_phase(control: qubit, target: qubit, angle(0.5))
phased_x(control: qubit, angle(1), angle(0.5))
phased_x(target: qubit, angle(-0.5), angle(-0.5))
rz(control: qubit, angle(-0.5))
rz(target: qubit, angle(0.5))
Controlled Z gate (CZ)¶
cz(control: qubit, target: qubit) is decomposed to
zz_phase(control: qubit, target: qubit, angle(0.5))
rz(target: qubit, angle(-0.5))
rz(control: qubit, angle(-0.5))
Helios Runtime¶
Helios employs specialized software running the control system. It enables the translation from operations on user program “virtual qubits” into operations on corresponding physical qubits in real time, whilst the program is executing and quantum state is live. The responsibility of this runtime is to efficiently map virtual qubits to physical qubits, and turn declarative gates on these virtual qubits into operations manipulating physical qubits. This runtime enables a state-of-the-art user programming experience for a quantum computer–functions that can allocate and deallocate qubits depending on the control flow of the program, early termination of programs based on MCMR or arbitrary classical logic - including classical control flow such as if-then-else statements, for loops, and while loops. The core responsibilities of the Helios runtime include:
receive qubit allocation requests on virtual qubits and resolve them to physical qubits;
receive gating requests on allocated virtual qubits;
determine how to transform requested gates on sets of virtual qubits into series of parallel operations on as many physical qubits as can fit in the quantum operation zones ;
efficiently transport batches of physical qubits from the ring into these zones, which uses junction transport and is referred to as “sort”.
Ion Transport¶
Quantinuum Helios uses dynamic ion transport. The ion transport is computed during real-time program execution and is dependent on conditional branching in a user’s program. A quantum runtime streams blocks of quantum gate operations to the hardware for execution and on-the-fly calculates ion transport. The overall transport is dynamic to the conditional branches in a user’s program. Dynamical transport can improve time to solution and reduce the strength of memory errors thus enabling larger and more effective QEC workflows.
Measurement Operations¶
Three types of measurements are used in the system some of which can be automatically chosen by the compiler while others are user selectable.
The standard measure occurs when the batch of ions in the gate zones are not all being measured. This measure induces crosstalk error.
Protected measure maps one of the hyperfine states in both qubits to multiple D\(_{\frac{5}{2}}\) manifold states so that all crosstalk pre-projects the qubit and the non-demolition nature of the manifolds protects from crosstalk errors.
Leakage measure allows the user to detect leakage error by shelving a qubit in the D\(_{\frac{5}{2}}\) manifold and subsequently in the D\(_{\frac{3}{2}}\). Furthermore, leakage and protected measure can be combined when an entire batch is measured.
Mid-circuit Measurement and Conditional Operations¶
Due to the internal level structure of trapped-ion qubits, a mid-circuit measurement may leave the qubit in a non-computational state. All mid-circuit measurements should be followed by initialization (MCMR) if the qubit is to be used again in that circuit. The qubit may be prepared in the measured state by calling for a measurement followed by initialization and a measurement dependent spin-flip.
When a subset of qubits is measured in the middle of the circuit, the classical information from these measurements can be used to condition future elements of the circuit via arbitrary control flow. Both gating operations and transport is dynamically determined in real-time based on the mid-circuit measurement outcome. Each branch in a program can include a different set of gating and transport operations.
The virtual qubit to ion mapping is a non-preserving map under implicit MCMR. This mapping can be preserved by using measure_and_reset as one unified operation, available in the module. See a discussion on MCMR.
Also available on Helios is a heralded leakage measurement operation, leakage_measure. This operation shelves the state of the barium qubit in a metastable state in the 2D\(_{\frac{5}{2}}\) spin manifold and performs measurements to determine leakage. The function returns a ternary outcome, {0, 1} if there is no leakage and 2 is there is leakage. The qubit must be reset after leakage_measure and converts leakage errors into erasure errors.
Hardware Credit Limitations¶
Each job submitted to hardware is limited to 10,000 shots and 500,000 Hardware Quantum Credits (HQCs) hard limit. Helios enables execution of programs with arbitrary control flow. As a consequence HQC consumption is dynamically determined in real time. Users must specify a max_cost parameter as a limit to control HQC spend per job.
Users are encouraged to contact Quantinuum to increase their HQC limits per shot.
Parameterized Angle ZZ Gates¶
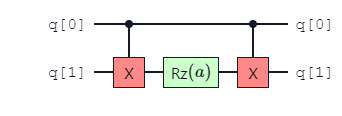
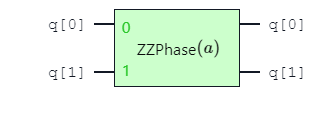
Although a parameterized angle 2-qubit entangling gate can be constructed using two fixed-angle 2-qubit entangling gates, a direct implementation will lower the error rate in the circuit. Not only is the number of entangling gates reduced, but the error of an \(RZZ(\theta)\) gate also scales with the angle \(\theta\) [1]. The error on \(R_{zz}(\frac{\pi}{2})\) is equal to the error of \(ZZ()\).
The gate sequence \(CX\), \(R_{z}\), \(CX\) can be replaced with the parameterized angle \(ZZ\) gate. This enables a lower number of 2-qubit gates in a quantum circuit, improving performance by decreasing gate errors.
For a narrative on parameterized angle gate usage, please see parameterized 2-qubit gates.
Real-time Classical Computation¶
The system enables server-side execution of real-time classical compute functions directly on the control system (ARM Cortex processor). The control system supports arbitrary classical computation including floating-point and integer arithmetic, boolean logic and an integrated Random Number Generator (RNG) capability. The control system also resolves arbitrary control flow logic in the user’s program and routes supported quantum operations to the Helios runtime.
Real-time QEC Decoding¶
A co-located low-latency, high-performance classical compute environment enables execution of user-defined table-driven or algorithmic QEC (Quantum Error Correction) decoders during the coherence time of qubits [1]. The classical compute environment uses a Wasm runtime, including a Wasm Virtual Machine (WAVM). It offers near-native execution speeds of custom decoders without requiring full-system modification. This environment is sand-boxed to protect against untrusted user code submitted for execution. The classical compute environment offers users 16GB RAM and leverages an Intel Kabylake processor, however parallelization is not possible with the Wasm runtime. Wasm execution requires network calls from the control system to the classical compute environment. A document on real-time QEC decoding is available here.
A low-latency Nvidia GPU Grace Hopper box, co-located with the control system, enables server-side QEC decoding using a GPU-driven blackbox belief-propagation ordered statistics decoding (BP-OSD) algorithm. The Wasm capability runs custom-defined, user-implemented decoder in real time. In contrast, the GPU integration restricts the user to 1 blackbox decoding algorithm which requires user-specific configurations. GPU decoding requires network calls from the control system.