Training: DisCoCirc¶
In Section From text to circuit, we saw how to convert entire paragraphs or even documents into quantum circuits using the experimental DisCoCircReader. In lambeq, these circuits can be trained as any other circuit using the standard trainers and models provided by the training module, and we’ll see a concrete example in this section.
For this purpose, we will use a variation of the meaning classification task introduced in [LPM+23], the goal of which was to classify simple sentences as related to IT or food. However, for this example, we will use a dataset of 300 small paragraphs, consisting of 3 sentences each. For example:
Man prepares tasty lunch.
He used to be a good chef.
He likes trying new recipes.
For our training, we will use the PennyLaneModel. We also use a Sim4Ansatz to convert the string diagrams into quantum circuits. When passing these circuits to the PennyLaneModel, they will be automatically converted into PennyLane circuits.
Preparation¶
We start by specifying some training hyperparameters and importing NumPy and PyTorch.
BATCH_SIZE = 10
EPOCHS = 30
LEARNING_RATE = 0.01
SEED = 42
import random
import numpy as np
import torch
torch.manual_seed(SEED)
random.seed(SEED)
np.random.seed(SEED)
Input data¶
Let’s read the data and print some example paragraphs.
def read_data(filename):
labels, sentences = [], []
with open(filename) as f:
for line in f:
t = float(line[0])
labels.append([t, 1. - t])
sentences.append(line[1:].strip())
return labels, sentences
train_labels, train_data = read_data('../examples/datasets/discocirc_mc_train_data.txt')
dev_labels, dev_data = read_data('../examples/datasets/discocirc_mc_dev_data.txt')
test_labels, test_data = read_data('../examples/datasets/discocirc_mc_test_data.txt')
train_data[:5]
['man bakes tasty lunch . he used to be a good shef . he likes mastering new recipes',
'woman writes efficient program . she has been a great professional . she likes mastering new approaches',
'girl writes nice software . she is a good coder . she likes mastering novel algorithms',
'person cooks tasty dinner . he was a modest professional . he likes trying new recipes',
'man prepares application . he used to be a great coder . he thrives in testing novel algorithms']
Targets are represented as 2-dimensional arrays:
train_labels[:5]
[[1.0, 0.0], [0.0, 1.0], [0.0, 1.0], [1.0, 0.0], [0.0, 1.0]]
Creating and parameterising diagrams¶
The first step is to convert the paragraphs into string diagrams. For that, we use the experimental DisCoCircReader class. Also, as explained in Section The “sandwich” functor, we need to replace the higher-order DisCoCirc frames into standard boxes by passing sandwich=True to the text2circuit() call to allow convertion to quantum circuits.
from lambeq.experimental.discocirc import DisCoCircReader
reader = DisCoCircReader()
raw_train_diags = [reader.text2circuit(t, sandwich=True) for t in train_data]
raw_dev_diags = [reader.text2circuit(t, sandwich=True) for t in dev_data]
raw_test_diags = [reader.text2circuit(t, sandwich=True) for t in test_data]
We can visualise these diagrams using draw() as usual.
raw_train_diags[0].draw(figsize=(5,10))
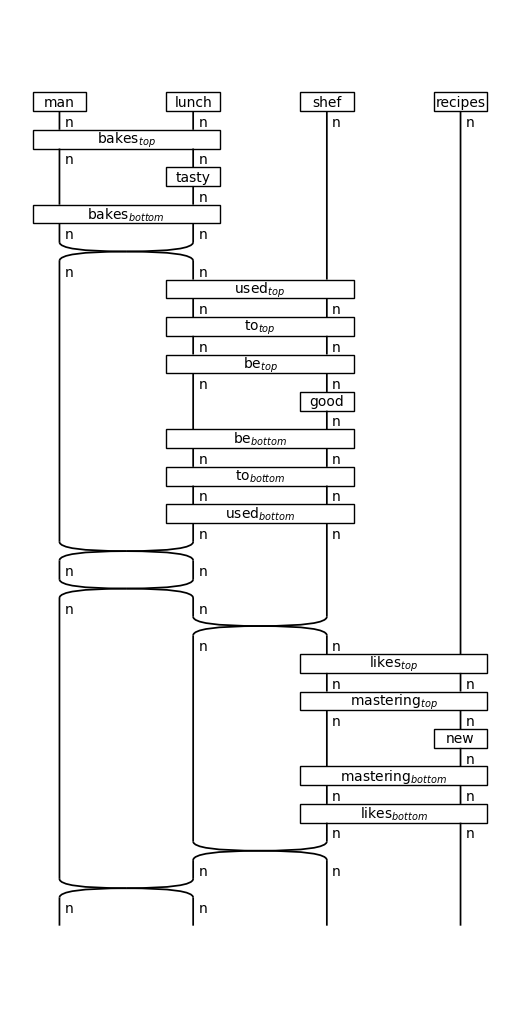
Get a single state for the circuit¶
For the specific task, we need a means to combine the output wires of the diagram and output a single wire that we will use for the prediction. This is easily done by adding a grammar.Box whose domain is the current diagram output and whose codomain is a single wire which we give the type t for text.
from lambeq import AtomicType
from lambeq.backend.grammar import Box, Ty
# Declare the types we will use
N = AtomicType.NOUN
T = Ty('t') # 't' for 'text'
# Add fan-in box as last layer for each diagram
def add_fan_in_box(diag):
fan_in_box = Box(name='fan in',
dom=diag.cod,
cod=T)
diag >>= fan_in_box
return diag
train_diags = [add_fan_in_box(d) for d in raw_train_diags]
dev_diags = [add_fan_in_box(d) for d in raw_dev_diags]
test_diags = [add_fan_in_box(d) for d in raw_test_diags]
train_diags[0].draw(figsize=(6, 10))
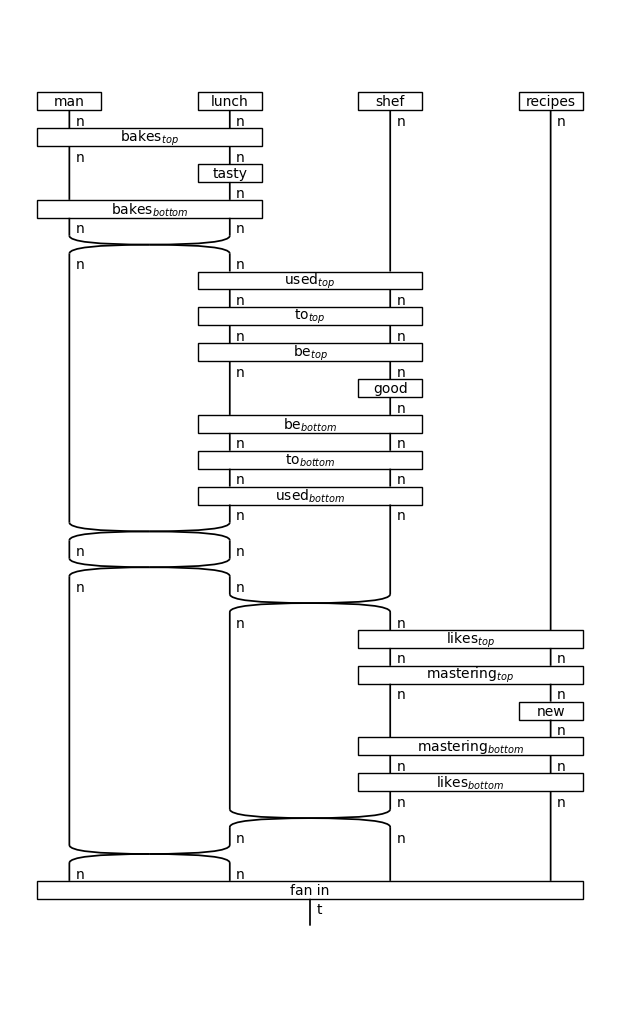
There will be several versions of this “fan in” box, varying only on the number of noun wires in their domain.
Create circuits¶
In order to run the experiments on a quantum computer, we apply a quantum ansatz to the string diagrams. As mentioned before, we will use a Sim4Ansatz, where noun wires (n) and text wires (t) are represented by one-qubit systems.
from lambeq import Sim4Ansatz
ansatz = Sim4Ansatz({N: 1, T: 1}, n_layers=3)
train_circs = [ansatz(diag) for diag in train_diags]
dev_circs = [ansatz(diag) for diag in dev_diags]
test_circs = [ansatz(diag) for diag in test_diags]
train_circs[0].draw(figsize=(24, 24))
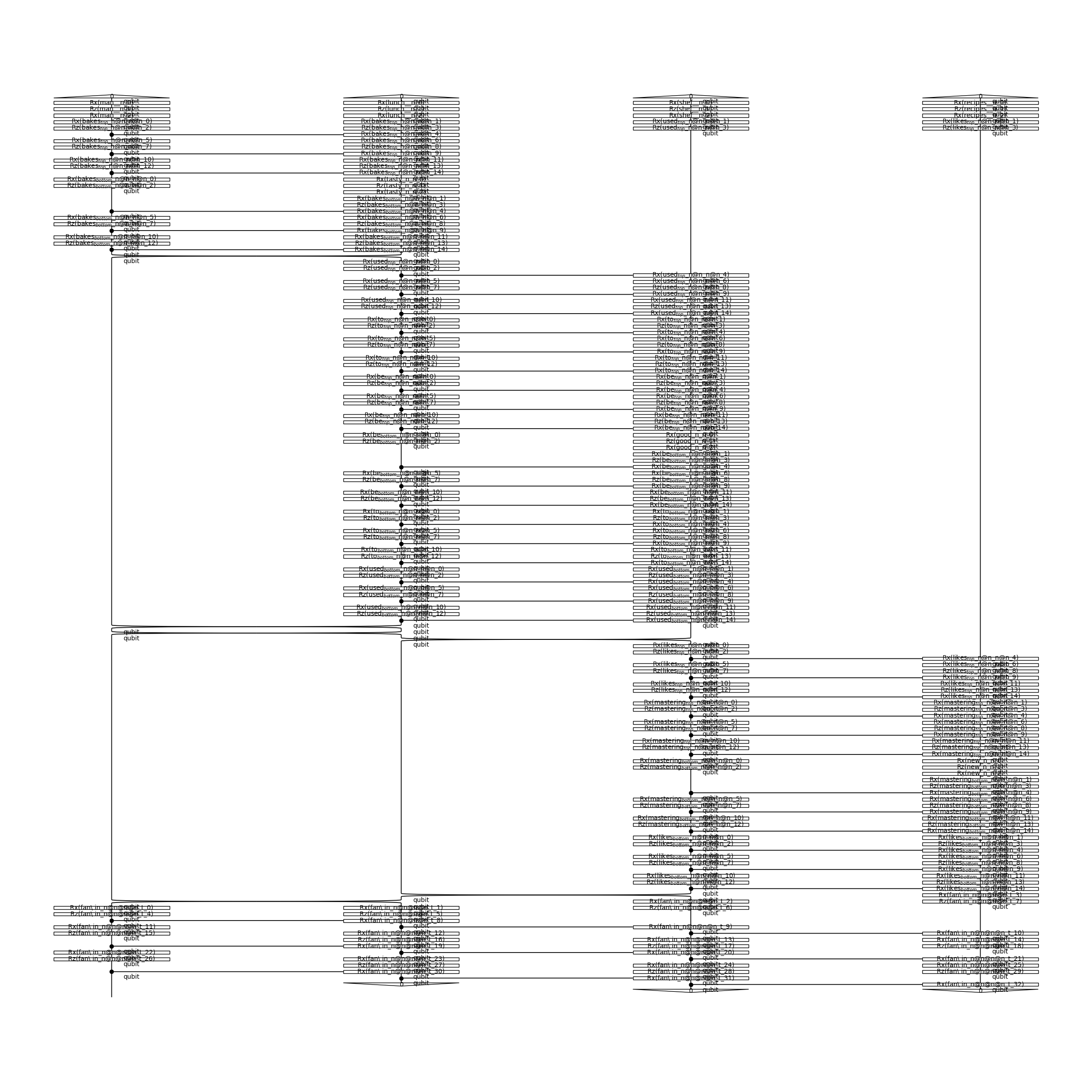
Training¶
Instantiate model¶
We instantiate a PennyLaneModel, by passing all diagrams to the class method from_diagrams(). We also set probabilities=True so that the model outputs probabilities, rather than quantum states, which follows the behaviour of real quantum computers. Furthermore, we set normalize=True so that the output probabilities sum up to one.
from lambeq import PennyLaneModel
all_circs = train_circs + dev_circs + test_circs
# if no backend_config is provided, the default is used
backend_config = {'backend': 'default.qubit'} # this is the default PennyLane simulator
model = PennyLaneModel.from_diagrams(all_circs,
probabilities=True,
normalize=True,
backend_config=backend_config)
model.initialise_weights()
Running this model on a real quantum computer takes a significant amount of time as the circuits must be sent to the backend and queued, so in this tutorial we will use the default PennyLane simulator, default.qubit.
Create datasets¶
To facilitate data handling and batching, lambeq provides a native Dataset class. Shuffling is enabled by default, and if not specified, the batch size is set to the length of the dataset.
from lambeq import Dataset
train_dataset = Dataset(train_circs,
train_labels,
batch_size=BATCH_SIZE)
dev_dataset = Dataset(dev_circs,
dev_labels,
shuffle=False)
Training can either by done using lambeq’s PytorchTrainer, or by using native PyTorch code. In this tutorial we will be using the first option, which is by far the most straightforward.
Define loss and evaluation metric¶
We first define our evaluation metrics and loss function, which in this case will be accuracy and binary cross entropy, respectively.
def acc(y_hat, y):
return (torch.argmax(y_hat, dim=1) ==
torch.argmax(y, dim=1)).sum().item()/len(y)
def loss(y_hat, y):
return torch.nn.functional.binary_cross_entropy(
y_hat, torch.Tensor(y)
)
Initialise trainer¶
As PennyLane is compatible with PyTorch autograd, PytorchTrainer can automatically use all of the PyTorch optimizers, such as Adam, to train our model.
from lambeq import PytorchTrainer
trainer = PytorchTrainer(
model=model,
loss_function=loss,
optimizer=torch.optim.Adam,
learning_rate=LEARNING_RATE,
epochs=EPOCHS,
evaluate_functions={'acc': acc},
evaluate_on_train=True,
use_tensorboard=False,
verbose='text',
seed=SEED)
Train¶
We can now pass the datasets to the fit() method of the trainer to start the training.
trainer.fit(train_dataset, dev_dataset)
Epoch 1: train/loss: 0.9695 valid/loss: 1.0455 train/time: 4m15s valid/time: 1m24s train/acc: 0.5000 valid/acc: 0.5000
Epoch 2: train/loss: 1.2423 valid/loss: 0.8468 train/time: 4m18s valid/time: 1m26s train/acc: 0.5167 valid/acc: 0.4500
Epoch 3: train/loss: 1.4184 valid/loss: 0.8690 train/time: 4m19s valid/time: 1m27s train/acc: 0.5333 valid/acc: 0.5667
Epoch 4: train/loss: 0.4773 valid/loss: 1.0767 train/time: 4m20s valid/time: 1m26s train/acc: 0.5889 valid/acc: 0.4333
Epoch 5: train/loss: 0.9689 valid/loss: 0.8239 train/time: 4m23s valid/time: 1m26s train/acc: 0.5333 valid/acc: 0.6000
Epoch 6: train/loss: 0.9354 valid/loss: 0.8176 train/time: 4m25s valid/time: 1m29s train/acc: 0.5333 valid/acc: 0.5500
Epoch 7: train/loss: 1.0967 valid/loss: 0.9583 train/time: 4m27s valid/time: 1m28s train/acc: 0.5222 valid/acc: 0.4500
Epoch 8: train/loss: 0.5902 valid/loss: 0.8774 train/time: 4m28s valid/time: 1m27s train/acc: 0.6222 valid/acc: 0.5500
Epoch 9: train/loss: 0.5998 valid/loss: 0.8630 train/time: 4m43s valid/time: 1m43s train/acc: 0.6389 valid/acc: 0.6000
Epoch 10: train/loss: 0.5799 valid/loss: 0.8210 train/time: 5m11s valid/time: 1m42s train/acc: 0.5889 valid/acc: 0.6167
Epoch 11: train/loss: 0.9772 valid/loss: 1.1537 train/time: 5m11s valid/time: 1m43s train/acc: 0.5722 valid/acc: 0.4333
Epoch 12: train/loss: 0.6276 valid/loss: 0.8586 train/time: 5m14s valid/time: 1m45s train/acc: 0.6167 valid/acc: 0.5667
Epoch 13: train/loss: 1.4431 valid/loss: 1.4355 train/time: 5m17s valid/time: 1m40s train/acc: 0.5222 valid/acc: 0.5000
Epoch 14: train/loss: 0.9701 valid/loss: 0.8888 train/time: 4m29s valid/time: 1m30s train/acc: 0.5889 valid/acc: 0.5667
Epoch 15: train/loss: 0.8250 valid/loss: 0.9828 train/time: 4m34s valid/time: 1m29s train/acc: 0.6667 valid/acc: 0.5167
Epoch 16: train/loss: 1.0572 valid/loss: 0.8387 train/time: 4m28s valid/time: 1m30s train/acc: 0.6500 valid/acc: 0.6167
Epoch 17: train/loss: 0.3985 valid/loss: 0.7681 train/time: 4m31s valid/time: 1m29s train/acc: 0.6667 valid/acc: 0.6333
Epoch 18: train/loss: 0.7628 valid/loss: 0.5444 train/time: 4m31s valid/time: 1m32s train/acc: 0.7722 valid/acc: 0.7667
Epoch 19: train/loss: 0.3056 valid/loss: 0.6176 train/time: 4m32s valid/time: 1m30s train/acc: 0.7611 valid/acc: 0.7167
Epoch 20: train/loss: 0.3587 valid/loss: 0.4453 train/time: 4m32s valid/time: 1m29s train/acc: 0.7667 valid/acc: 0.8500
Epoch 21: train/loss: 0.2189 valid/loss: 0.5145 train/time: 4m32s valid/time: 1m29s train/acc: 0.8333 valid/acc: 0.8000
Epoch 22: train/loss: 0.1592 valid/loss: 0.3655 train/time: 4m31s valid/time: 1m31s train/acc: 0.8167 valid/acc: 0.8667
Epoch 23: train/loss: 0.1945 valid/loss: 0.2800 train/time: 4m32s valid/time: 1m30s train/acc: 0.9167 valid/acc: 0.9167
Epoch 24: train/loss: 0.0599 valid/loss: 0.1828 train/time: 4m33s valid/time: 1m34s train/acc: 0.9722 valid/acc: 0.9000
Epoch 25: train/loss: 0.1717 valid/loss: 0.1657 train/time: 4m35s valid/time: 1m31s train/acc: 0.9778 valid/acc: 0.9500
Epoch 26: train/loss: 0.0121 valid/loss: 0.1378 train/time: 4m37s valid/time: 1m31s train/acc: 0.9944 valid/acc: 0.9667
Epoch 27: train/loss: 0.0367 valid/loss: 0.0807 train/time: 4m40s valid/time: 1m33s train/acc: 1.0000 valid/acc: 0.9667
Epoch 28: train/loss: 0.0038 valid/loss: 0.1031 train/time: 4m36s valid/time: 1m37s train/acc: 1.0000 valid/acc: 0.9833
Epoch 29: train/loss: 0.0083 valid/loss: 0.0597 train/time: 4m38s valid/time: 1m34s train/acc: 1.0000 valid/acc: 1.0000
Epoch 30: train/loss: 0.0065 valid/loss: 0.0595 train/time: 4m34s valid/time: 1m32s train/acc: 1.0000 valid/acc: 1.0000
Training completed!
train/time: 2h17m57s train/time_per_epoch: 4m36s train/time_per_step: 15.33s valid/time: 45m57s valid/time_per_eval: 1m32s
Results¶
Finally, we visualise the results and evaluate the model on the test data.
import matplotlib.pyplot as plt
fig, ((ax_tl, ax_tr), (ax_bl, ax_br)) = plt.subplots(2, 2,
sharex=True,
sharey='row',
figsize=(10, 6))
ax_tl.set_title('Training set')
ax_tr.set_title('Development set')
ax_bl.set_xlabel('Iterations')
ax_br.set_xlabel('Iterations')
ax_bl.set_ylabel('Accuracy')
ax_tl.set_ylabel('Loss')
colours = iter(plt.rcParams['axes.prop_cycle'].by_key()['color'])
range_ = np.arange(1, trainer.epochs+1)
ax_tl.plot(range_, trainer.train_epoch_costs, color=next(colours))
ax_bl.plot(range_, trainer.train_eval_results['acc'], color=next(colours))
ax_tr.plot(range_, trainer.val_costs, color=next(colours))
ax_br.plot(range_, trainer.val_eval_results['acc'], color=next(colours))
# print test accuracy
pred = model(test_circs)
labels = torch.tensor(test_labels)
print('Final test accuracy: {}'.format(acc(pred, labels)))
Final test accuracy: 0.9666666666666667
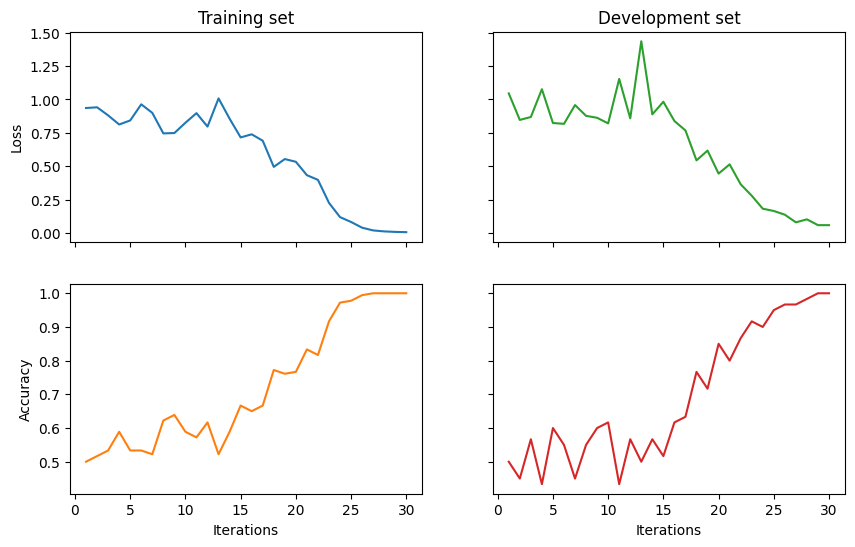
See also: